In NLP we represent words with numbers. Each word has its own unique number. So how do we assign numbers to words? Can we start from 'a', go through the dictionary and give each word a unique number? So 'a' becomes 1 and 'zulu' (assuming the last word of the dictionary) becomes 100,000 (assuming there are 100k words in the english dictionary). Although this satisfies our condition of giving each word a unique number, it turns out ML models don't really perform well with this approach.
Example: Let's take "beer" and "Beethoven". If we give them numbers based on their position in the dictionary, they would be quite close to each other. But we want our ML model to understand that "beer" is close to some other words such as "wine" and "bar". "Beethoven" should be close to word such as "Music" and "piano".
One other way to represent words with numbers is using one-hot-encoding. Each word will be a one-hot vector.
Example:
apple = [0 0 0 0 0 0 1 0 0 0]
banana = [0 0 0 0 0 0 0 0 1 0]
bed = [0 1 0 0 0 0 0 0 0 0]We would like computer to understand that apple and banana are closer to each other than they are to bed. However, those 3 one-hot vectors are orthogonal, in other words, there is no notion of similarity for one-hot vectors.
Can we somehow capture the fact that apple and banana are similar and bed is different.
Solution: Word2vec
Word2vec Algorithm
Word2vec is a framework for learning word vectors.
It uses a simple idea: A word's meaning is given by the words that frequently appear close-by.
Idea of Word2vec can be summarized as:
- We have a large corpus of text and each word is represented by a vector
- Determine a window length (w)
- Go through each word in the corpus
- Current word becomes our center word
- Words that are in -w, +w window become context word
- Calculate the probability of finding the context word in the window given our center word using the similarity of word vectors
- Adjust the word vectors to maximize the probability
Example:
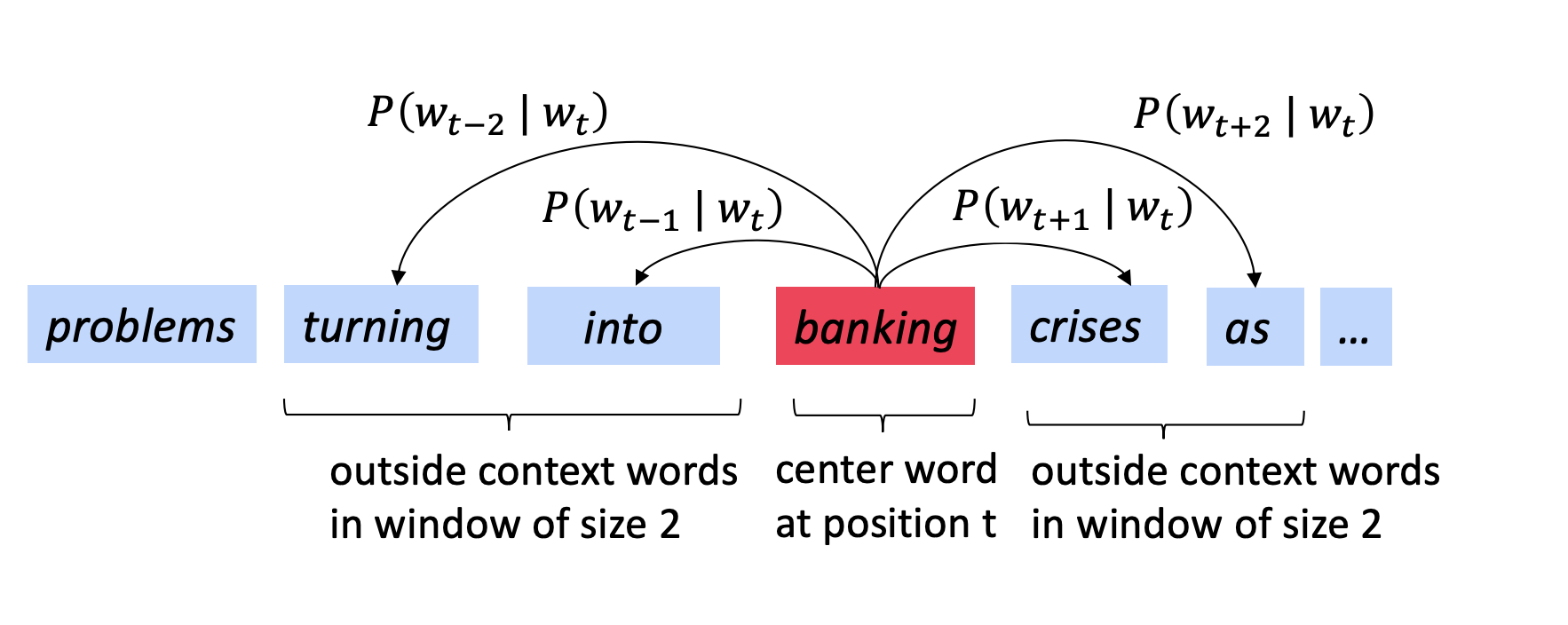
In this approach we have one objective: maximize the probability of given center word, finding context words. If we put a negative in front of this objective function we have a minimization problem, in other words, we have a loss function.
Loss Function
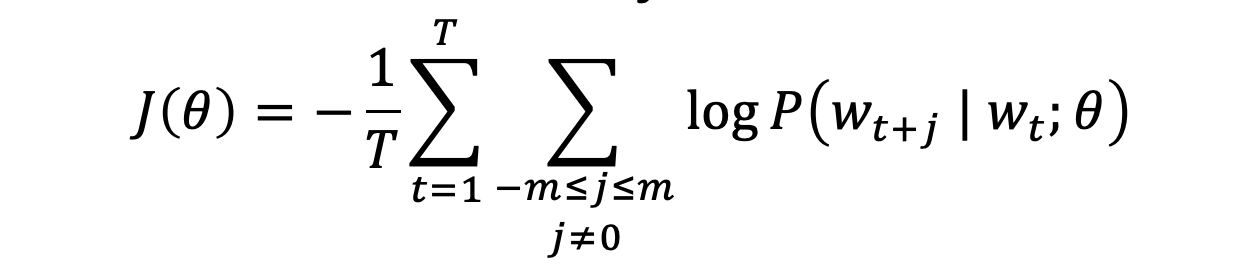
This equation above is nothing but a mathematical representation of the Word2vec Idea listed above. But there is one problem: How to determine the given center word probability of finding context word?
Answer: Softmax
For a center word c and a context word o probability can be calculated using the equation below:
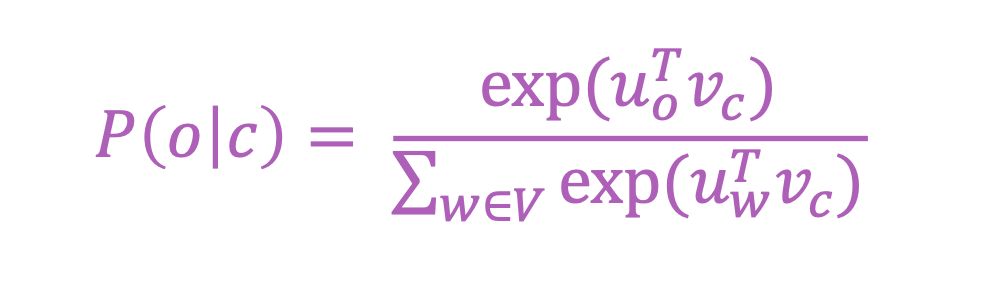
Notice that there are two vectors here u and v. u is used for the center word and v is used for context word. So there will be two vectors for each word. At the end we will average the two vectors to find vector representation of the words.The reason we use two vectors instead of just one is that it makes optimization easier but we can do the same thing with just one vector per word too.
So far we implemented skip-gram version: Predict the context words given center word.
The other variant is Continuous Bag of Words (CBOW): Predict center word from (bag of) context words.
In the loss function we have the softmax which requires calculating the probability of all the possible pairs which is quite computationally expensive. So a less complex way is to use negative sampling.
Negative Sampling
Negative Sampling: Instead of calculating all the probabilities, we sample some number of random words and distinguish target word from the sampled random words using a logistic regression. Usually we sample 5 to 15 negative examples. In the original word2vec paper, the best results are achieved with 15 negative examples. The new loss function with negative sampling can be seen below.
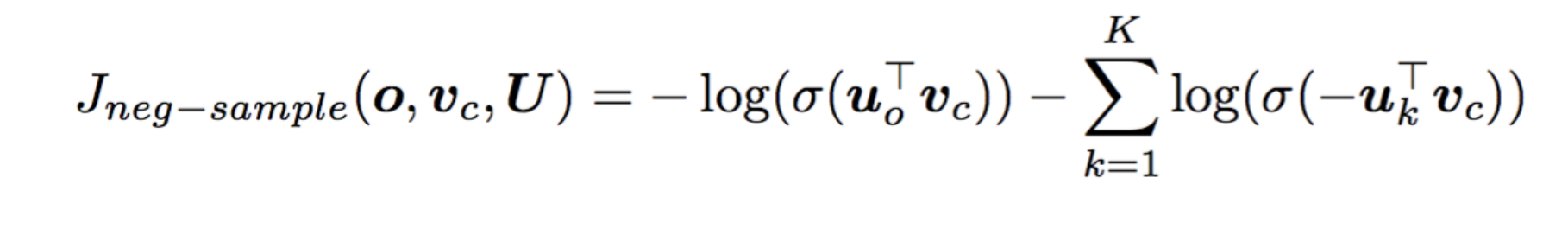
The interpretation of the new loss function is fairly easy. We want the first log to be big (real context words) and second log to be small (randomly sampled words) so with this new loss function our model learns word vectors without calculation all possible combination for that center word at each step.
Last Notes
- Word2vec was created and published in 2013 by a team of researchers led by Tomas Mikolov at Google. Their two papers which can be found here and here, have been cited in the scientific literature 17231 and 21670 times, respectively (Google Scholar, 2 Aug 2020). I suggest you to go and have a look at these papers.
- One alternative approach to word2vec is GloVe which is created by Stanford NLP Group. I am planning to cover it in another blog post.